Вы узнаете, может ли правило преобразования клеточек кодируемое 8 битами быть Тьюринг полным, хаотичным и даже полезным.

Что такое клеточный автомат?

Клеточный автомат в общем случае это просто правило преобразования одного массива клеточек в другой. Клеточки в этом массиве могут быть либо белыми (кодируются нулем), либо черными (кодируются единицами).

Вы наверняка слышали про двумерный клеточный автомат под названием “Игра Жизнь“ (он, кстати, тоже Тьюринг полный, почитайте больше на вики).

Что такое элементарный клеточный автомат?

Элементарные клеточные автоматы являются самым простым подвидом всех клеточных автоматов, однако это не мешает им создавать сложные и интересные структуры. Представьте, что у вас есть некоторая лента N x 1 (именно поэтому такие автоматы еще называются одномерными, а N в математическом случае равно бесконечности), и, основываясь на совокупности черных и белых клеток (единиц и нулей), вы создаете новую ленту. Расположите ее под старой лентой и для каждой клетки рассмотрите ее трех ближайших соседей сверху. Всего может быть 8 комбинаций (111, 110, 101, 100, 011, 010, 001, 000). Для каждой комбинации клетка может стать либо единицей, либо нулем, поэтому всего таких автоматов может быть 2^8 = 256. Таким образом каждый автомат можно закодировать числом в отрезке [0, 255]. Это называется кодом Вольфрама (да, это он сделал Wolfram Alpha и Mathematica).

Будем брать в качестве начальной ленты полоску с нулями и одной единицей посередине (...000010000...) и каждую итерацию будем брать нижнюю полоску и получать новую по правилу с кодом Вольфрама. Так будет получаться черно-белая картинка, по которой можно анализировать поведение правила.

Итак, к примерам:

Я написал небольшую страничку, чтобы вы могли попробовать разные правила своими руками: zpix1.github.io/cellular-automaton-showroom. Картинки далее сгенерированы именно ей.

Правило 90

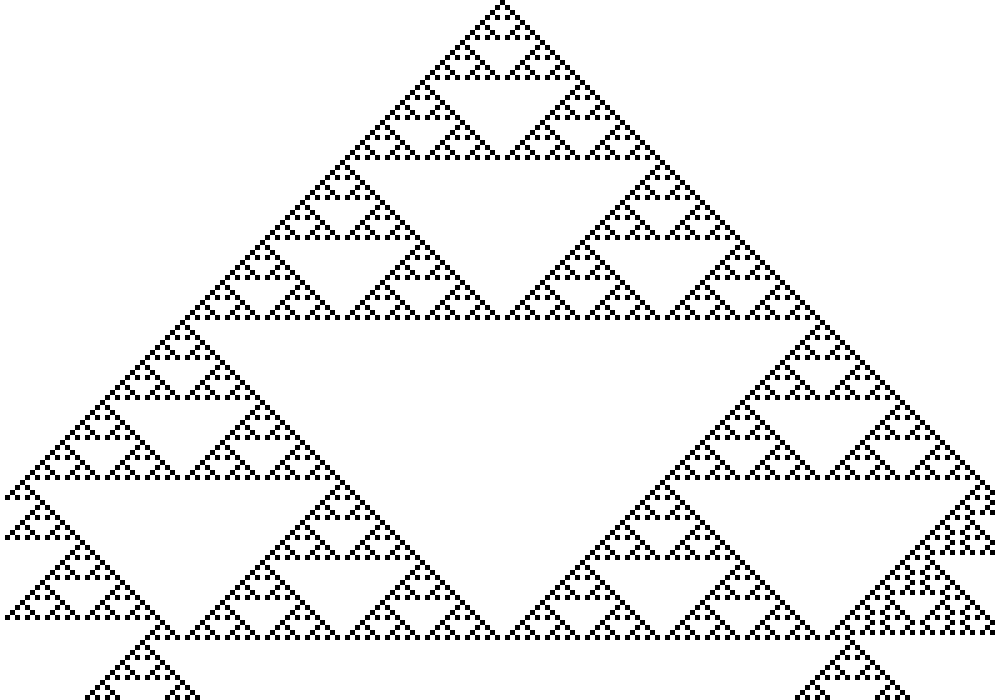
Треугольник Серпинского!?

Правило 73

Тут за начальную позицию взята случайная полоска, так получается лучше.

У меня эта картинка ассоциируется с многоэтажными домами, а у вас?

Правило 30

Тут размер ячейки уменьшен в 5 раз.

Как видно, в левой части пирамиды сохраняется некоторый порядок, но в правой ситуация становится абсолютно непонятной (и так можно даже генерировать случайные числа).

Из простейшего правила и всего лишь одной единицы получилась огромная хаотичная пирамида. Разве это не удивительно?

Правило 110

Тут пирамида растет влево, поэтому за единичную взята самая правая ячейка начальной ленты.

Как видно, левая сторона пирамиды является периодической, в то время как ее середина не имеет каких-то выраженных паттернов.

Это правило является Тьюринг полным, то есть контролируя начальную полоску можно сосчитать любую функцию (интуитивно вычислимую), это значит можно реализовывать циклы и простейшие арифметические операции. Однако никто не говорил, что это будет легко и программы на таком своеобразном языке программирования могут оказаться очень и очень громоздкими.

Где узнать больше?

В википедии, рекомендую английскую: Elementary cellular automaton;

Книгу и сайт Стивена Вольфрама: Книга - Наука нового типа, Wolfram MathWorld;